17. 卦長故事-序章
0 Judge
Code: 0
卦長故事-序章
題目敘述
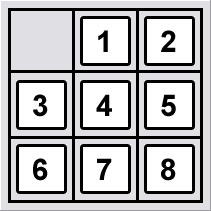
ㄠㄨ
卦長將8數字拼盤的問題,交給你來解解看。8數字拼盤的規則如下:
- 這是一個3*3的方格作為起始盤面,每個格子裡面都有0~8不重複的數字
- 編號0的格子可以隨時跟它周圍(上下左右,如果有格子的話)的格子交換位置,交換一次記為一個步驟
- 給你一個目標盤面,去計算起始盤面變成目標盤面最少需要幾個步驟
- 有可能跟卦長那永遠都解不開的迷一樣,會出現無解的情況
輸入說明
第一行有一個數字$T,\; 1 \leq T \leq 20$,下一行接著會有一個3*3的格子做為目標盤片,接著會有$T$個3*3的格子做為起始盤面。
輸出說明
按造輸入順序,對於每個起始盤面,如果不能透過規則變成目標盤片,則輸出MS並換行;反之輸出該起始盤面變成目標盤面最少需要幾個步驟。
範例輸入
3
1 5 6
3 7 8
4 2 0
7 1 8
6 4 2
3 5 0
2 3 1
5 7 6
4 8 0
1 5 6
3 7 8
4 2 0
範例輸出
MS
18
0
配分方法
- 20% $T \leq 5$
- 20% $T \leq 10$
- 20% $T \leq 15$
- 40% $T \leq 20$
提示
無解的情況要用數學的方法判斷掉喔備註
我會抓抄襲喔Judge Setting
run-time limit: 2000 msmemory limit: 16553600 byte
測資數量: 0